Semi-infinite Hodge structure: from BCOV theory to Seiberg-Witten geometry - Si Li

Semi-infinite Hodge structure: from BCOV theory to Seiberg-Witten geometryПодробнее

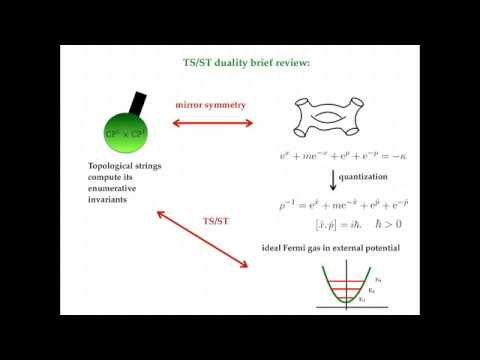
Seiberg-Witten theory as a Fermi gasПодробнее

Andriy Haydys - G₂ instantons and the Seiberg Witten monopolesПодробнее

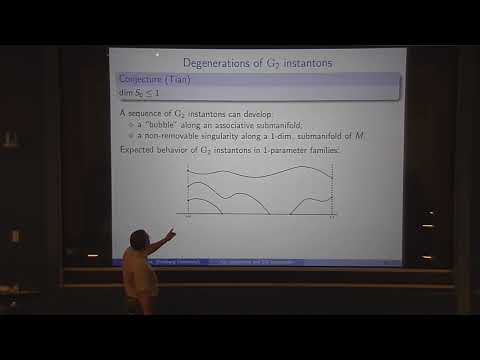
Andriy Haydys - On degenerations of the Seiberg–Witten monopoles and G₂ instantonsПодробнее

Integrable systems and Seiberg-Witten geometryПодробнее

Semi-infinite hodge structure: from BCOV theory to Seiberg-Witten geometryПодробнее

K. Costello - An overview of BCOV theory and its quantization IПодробнее

Dmytro Shklyarov: Semi-infinite Hodge structures in noncommutative geometryПодробнее

Calabi-Yau geometry, Kodaira-Spencer gravity and integrable hierarchyПодробнее

JDG 2017: Si Li: Vertex algebras, quantum master equation and mirror symmetryПодробнее

Si Li | Elliptic chiral homology and quantum master equationПодробнее

Josè Francisco Morales Lecture IVПодробнее

Matthias Traube - Seiberg-Witten maps and L1-quasi-isomorphismsПодробнее

Introduction to Seiberg-Witten Theory - Dr Elli Pomoni (Lecture 3)Подробнее

Andriy Haydys - Seiberg-Witten monopoles and flat PSL(2,R) connectionsПодробнее

Lefschetz theorems beyond Hodge structures, Lecture OneПодробнее

Brandon Levin: The weight part of Serre's conjecture and the Emerton-Gee stackПодробнее