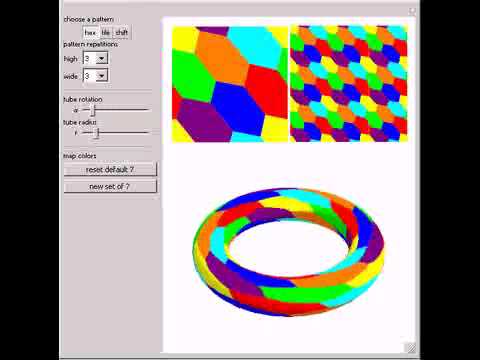
A map on the torus that cannot be colored in 6 colors.
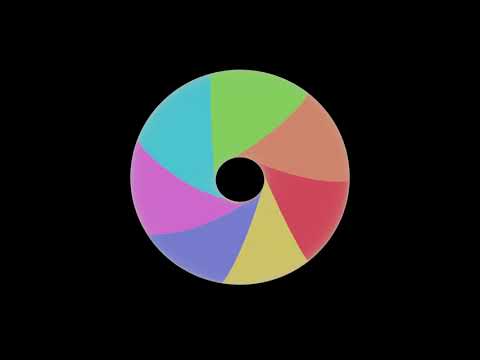
Map Coloring on a TorusПодробнее
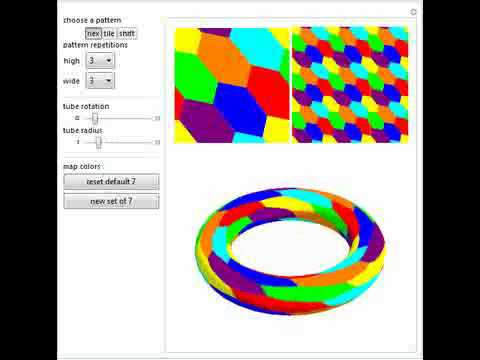
Seven-Coloring of a TorusПодробнее
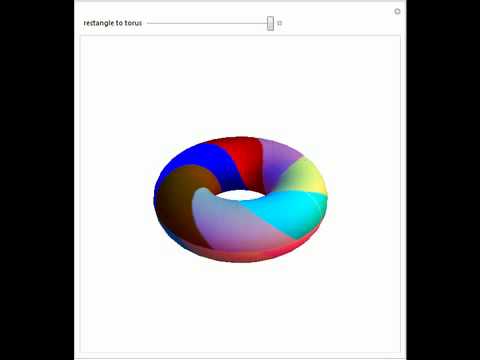
Four Color Theorem - non-four-colorable mapПодробнее
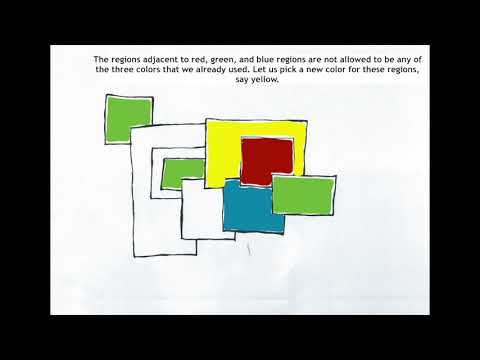
Four Colors, ANY Map!Подробнее

Map Coloring on a TorusПодробнее
The Four Color Map Theorem - NumberphileПодробнее

Why is 4-color theorem easier on a torus?Подробнее

Topology of Graph ColoringПодробнее

The Four Color TheoremПодробнее

Paradigms 9 | Colouring Maps on Surfaces: A Glimpse of TopologyПодробнее

Map Coloring TheoremsПодробнее

How Many Colors Do Maps Need? #shortsПодробнее
The Four Colour TheoremПодробнее

87/365 Coloring the World | The Four Color Theorem Explained #shorts #365daysofmathПодробнее
The four color map theorem! #math #learning #learneclecticthingsПодробнее

Math's Map Coloring Problem - The First Proof Solved By A ComputerПодробнее

Math Encounters: Color My World: making modular origami map coloring models — E. Torrence 11/2/2022Подробнее

The Mathematics Behind Map ColouringПодробнее
